რა განსხვავებაა ყუთისა და ულვაშის ნაკვეთსა და ყუთის ნაკვეთს შორის?

2024 ავტორი: Lynn Donovan | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:49

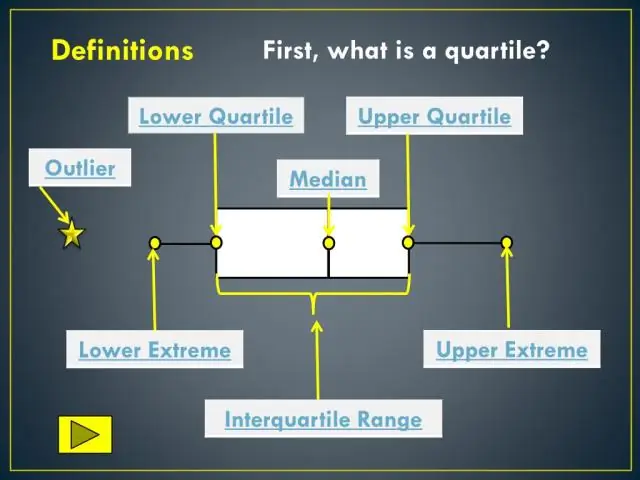
ა ყუთი და ულვაშის ნაკვეთი (ზოგჯერ ეძახიან ა ყუთი ) არის გრაფიკი რომელიც წარმოადგენს ინფორმაციას ხუთნომრიანი შეჯამებიდან. ყუთში და ულვაში : ბოლოები ყუთი არის ზედა და ქვედა კვარტილები, ასე რომ ყუთი მოიცავს ინტერკვარტულ დიაპაზონს. მედიანა აღინიშნება ვერტიკალური ხაზით შიგნით ყუთი.

ამასთან დაკავშირებით, რას ნიშნავს ყუთი და ულვაშის ნაკვეთი?

ა ყუთი და ულვაშის ნაკვეთი განისაზღვრება, როგორც გრაფიკული მეთოდი მონაცემების ერთობლიობაში ცვალებადობის ჩვენების. უმეტეს შემთხვევაში, ჰისტოგრამის ანალიზი იძლევა საკმარის ჩვენებას, მაგრამ ა ყუთი და ულვაშის ნაკვეთი შეუძლია დამატებითი დეტალების მიწოდება, ხოლო მონაცემთა მრავალრიცხოვანი ნაკრების ერთსა და იმავე გრაფიკში ჩვენების უფლება.

ასევე, როგორ გამოვთვალოთ ყუთის ნაკვეთი? შესაქმნელად ა ყუთი -და-ულვაში ნაკვეთი , ვიწყებთ ჩვენი მონაცემების შეკვეთით (ანუ მნიშვნელობების დაყენებით) რიცხვითი თანმიმდევრობით, თუ ისინი უკვე შეკვეთილი არ არის. შემდეგ ჩვენ ვიპოვით ჩვენი მონაცემების მედიანას. მედიანა მონაცემებს ორ ნაწილად ყოფს. მონაცემების მეოთხედებად დასაყოფად, შემდეგ ვიპოვით ამ ორი ნახევრის მედიანას.

ასევე იცით, რას გვეუბნება ყუთების ნაკვეთები?

ა ყუთი არის მონაცემთა განაწილების ჩვენების სტანდარტიზებული გზა, რომელიც დაფუძნებულია ხუთ რიცხვიან შეჯამებაზე („მინიმუმი“, პირველი მეოთხედი (Q1), მედიანა, მესამე მეოთხედი (Q3) და „მაქსიმუმი“). ის შეუძლია გითხრათ თქვენ შესახებ თქვენი outliers და რა არის მათი ღირებულებები.

როგორ განვსაზღვროთ გამოკვეთილები?

წერტილი, რომელიც ხვდება მონაცემთა ნაკრების შიდა ღობეებს მიღმა, კლასიფიცირდება როგორც უმნიშვნელო გამოკვეთილი , ხოლო ის, რომელიც გარე ღობეებს გარეთ ხვდება, კლასიფიცირებულია, როგორც ძირითადი გამოკვეთილი . რომ იპოვე შიდა ღობეები თქვენი მონაცემთა ნაკრებისთვის, ჯერ გაამრავლეთ ინტერკვარტილური დიაპაზონი 1.5-ზე. შემდეგ, დაამატეთ შედეგი Q3-ს და გამოაკელი Q1-ს.