
- ავტორი Lynn Donovan [email protected].
- Public 2023-12-15 23:49.
- ბოლოს შეცვლილი 2025-01-22 17:29.
ორობითი საძიებო ხის (BST) დანერგვა ჯავაში
- კვანძის მარცხენა ქვეხე შეიცავს მხოლოდ კვანძებს, რომელთა კლავიშები ნაკლებია კვანძის გასაღებზე.
- კვანძის მარჯვენა ქვეხე შეიცავს მხოლოდ კვანძებს, რომელთა კლავიშები აღემატება კვანძის კლავიშს.
- მარცხენა და მარჯვენა ქვეხე ასევე უნდა იყოს a ორობითი საძიებო ხე .
- არ უნდა იყოს დუბლიკატი კვანძები.
ასევე კითხვაა, როგორ ხდება ორობითი ძებნა ჯავაში?
ვნახოთ ორობითი ძიების მაგალითი java-ში, სადაც ვაპირებთ მასივიდან ელემენტის მოძიებას რეკურსიის გამოყენებით
- კლასი BinarySearchExample1{
- საჯარო სტატიკური int binarySearch(int arr, int პირველი, int ბოლო, int გასაღები){
- თუ (ბოლო>=პირველი){
- int mid = პირველი + (ბოლო - პირველი)/2;
- თუ (arr[mid] == გასაღები){
- შუა რიცხვებში დაბრუნება;
- }
მეორეც, სად ვიყენებთ ბინარული საძიებო ხეს? ორობითი საძიებო ხე - Გამოყენებული ბევრში ძებნა აპლიკაციები, სადაც მონაცემები მუდმივად შედის/გადის, როგორიცაა რუკა და კომპლექტის ობიექტები მრავალი ენის ბიბლიოთეკაში. ორობითი კოსმოსური დანაყოფი - Გამოყენებული თითქმის ყველა 3D ვიდეო თამაშში იმის დასადგენად, თუ რა ობიექტებია საჭირო რენდერით.
ასე რომ, როგორ იქმნება ბინარული ხეები?
ორობითი ხის შექმნა რეკურსიის გამოყენებით
- წაიკითხეთ მონაცემები x-ში.
- გამოყავით მეხსიერება ახალი კვანძისთვის და შეინახეთ მისამართი პოინტერში p.
- შეინახეთ მონაცემები x კვანძში p.
- რეკურსიულად შექმენით p-ის მარცხენა ქვეხე და გახადეთ იგი p-ის მარცხენა შვილად.
- რეკურსიულად შექმენით p-ის მარჯვენა ქვეხე და გახადეთ იგი p-ის სწორ შვილად.
რა არის ორობითი ძიების სირთულე?
ორობითი ძებნა გადის ყველაზე ცუდ ლოგარითმულ დროს, აკეთებს O(log n) შედარებებს, სადაც n არის მასივის ელემენტების რაოდენობა, O არის Big O აღნიშვნა და log არის ლოგარითმი. ორობითი ძებნა იღებს მუდმივ (O(1)) სივრცეს, რაც იმას ნიშნავს, რომ ალგორითმის მიერ აღებული სივრცე იგივეა მასივის ნებისმიერი რაოდენობის ელემენტისთვის.
გირჩევთ:
როგორ გავააქტიურო საძიებო ველი Windows 10-ში?
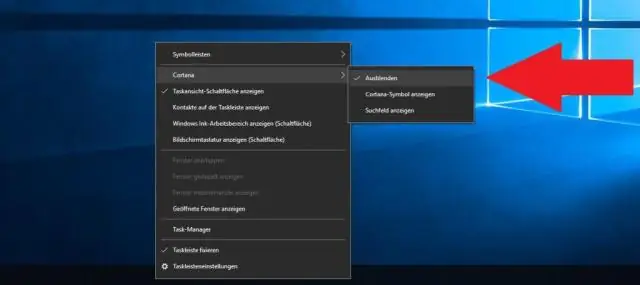
თუ თქვენი საძიებო ზოლი დამალულია და გსურთ, რომ ის აჩვენოს დავალების პანელზე, ხანგრძლივად დააჭირეთ (ან დააწკაპუნეთ მარჯვენა ღილაკით) ამოცანების ზოლზე და აირჩიეთ ძიება > საძიებო ველის ჩვენება
როგორ დავამატო საძიებო ხატი ტექსტის ველში HTML-ში?

როგორ შევქმნათ ტექსტური ყუთი საძიებო ხატით HTML და CSS-ში? ნაბიჯი 1: შექმენით index.html მისი ძირითადი სტრუქტურით. <! დაამატეთ შეყვანის ველი ტეგის შიგნით. ასევე ჩართეთ ადგილის დამჭერი, რომელიც ამბობს „ძებნა“ნაბიჯი 3: ჩამოტვირთეთ საძიებო ხატულა. ნაბიჯი 4: დაამატეთ div სურათის ხატულა შიგნით. ნაბიჯი 5: დაამატეთ ჯადოსნური CSS
რა არის საძიებო სისტემები, რომლებიც ეძებენ სხვა საძიებო სისტემებს?
ჩვენი საძიებო თავგადასავლის დასაწყებად, მოდით გადავხედოთ რამდენიმე ზოგად საძიებო სისტემას სამეულს მიღმა. DuckDuckGo. გაინტერესებთ ონლაინ კონფიდენციალურობა? ძიება Encrypt. ეძებთ DuckDuckGo-ს ალტერნატივას? ეკოსია. გსურთ ხეების დარგვა სანამ ეძებთ? Dogpile. ბლეკო. ვოლფრამალფა. გიგაბლასტი. ფეისბუქის ძებნა
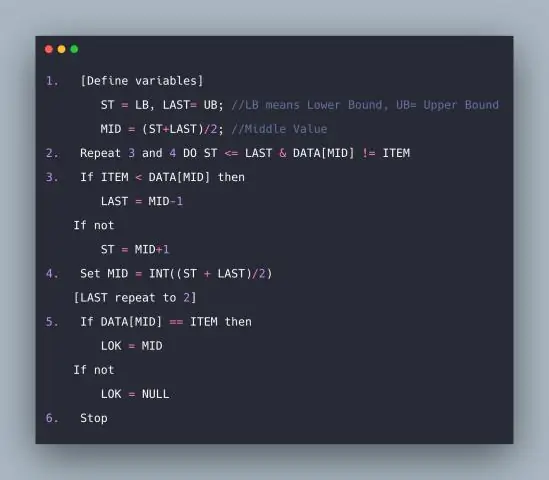
როგორ პოულობთ ორობითი ძიების შუა რიცხვებს?
დახარისხებული მასივის გათვალისწინებით, ჩვენ ვპოულობთ ყველაზე შუა ელემენტს და ვამოწმებთ ელემენტს გასაღებით. თუ ყველაზე შუა ელემენტი გასაღების ტოლია, ჩვენ ვიპოვნეთ გასაღები. თუ ყველაზე შუა ელემენტი კლავიშზე დიდია, ჩვენ ვეძებთ ყველაზე შუა ელემენტის მარცხენა ნახევარში, წინააღმდეგ შემთხვევაში ვეძებთ მარჯვენა ნახევარში
რა არის საძიებო სისტემა ჯავაში?
Lucene არის კანონიკური Java საძიებო სისტემა. სხვადასხვა წყაროდან დოკუმენტების დასამატებლად, გადახედეთ Apache Tika-ს და სერვისის/ვებ ინტერფეისების სრულფასოვან სისტემას, solr. Lucene საშუალებას აძლევს თვითნებური მეტამონაცემების ასოცირებას მის დოკუმენტებთან. თიკა ავტომატურად ამოიღებს მეტამონაცემებს სხვადასხვა ფორმატიდან
