ვიდეო: რატომ არის სასარგებლო ტრიგონომეტრიული იდენტობები განტოლებების ამოხსნისას?
2024 ავტორი: Lynn Donovan | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:49
იდენტობები საშუალებას გვაძლევს გავამარტივოთ რთული გამონათქვამები. ისინი ძირითადი ინსტრუმენტებია ტრიგონომეტრია, რომელიც გამოიყენება ტრიგონომეტრიული განტოლებების ამოხსნისას , ისევე როგორც ფაქტორინგი, საერთო მნიშვნელების პოვნა და სპეციალური ფორმულების გამოყენება არის ძირითადი ინსტრუმენტები გადაჭრა ალგებრული განტოლებები.
მაშინ, რა ხდის ტრიგონომეტრიულ განტოლებას იდენტურად?
მათემატიკაში, ტრიგონომეტრიული იდენტობები არის თანასწორობა, რომელიც მოიცავს ტრიგონომეტრიული ფუნქციები და ჭეშმარიტია წარმოქმნილი ცვლადების ყველა მნიშვნელობისთვის, სადაც განისაზღვრება ტოლობის ორივე მხარე. გეომეტრიულად, ესენი არიან ვინაობა მოიცავს ერთი ან რამდენიმე კუთხის გარკვეულ ფუნქციებს.
ასევე იცით, რა არის ტრიგონომეტრიული განტოლებები? ა ტრიგონომეტრიული განტოლება არის ნებისმიერი განტოლება რომელიც შეიცავს ა ტრიგონომეტრიული ფუნქცია. როგორც აღნიშნულია ტრიგონომეტრიული იდენტობები, ა ტრიგონომეტრიული განტოლება რომელიც მართებულია ნებისმიერი კუთხისთვის, ეწოდება a ტრიგონომეტრიული ვინაობა. არის სხვა განტოლებები თუმცა, ეს მართალია მხოლოდ გარკვეული კუთხით.
ანალოგიურად შეიძლება ვინმემ იკითხოს, რა არის ტრიგონომეტრიული იდენტობების ამოხსნის ყველაზე მარტივი გზა?
ნაბიჯი 1: გადააკეთეთ ყველა წამი, csc, cot და tan sin და cos. ამის უმეტესობა შეიძლება გაკეთდეს კოეფიციენტისა და ორმხრივი გამოყენებით ვინაობა . ნაბიჯი 2: შეამოწმეთ ყველა კუთხე ჯამებისთვის და სხვაობებისთვის და გამოიყენეთ შესაბამისი ვინაობა მათ მოსაშორებლად. ნაბიჯი 3: შეამოწმეთ კუთხის ჯერადები და ამოიღეთ ისინი შესაბამისი ფორმულების გამოყენებით.
რას უდრის ცოდვა 2x?
sin2x =( ცოდვა x)2=12(1−cos( 2x )).
გირჩევთ:
რატომ არის საქმეების დიაგრამები სასარგებლო?
ერთიანი მოდელირების ენის (UML) გამოყენებისას გამოყენების შემთხვევების დიაგრამა გეხმარებათ გაიგოთ, როგორ შეუძლია მომხმარებელმა ურთიერთქმედება თქვენ მიერ შემუშავებულ სისტემასთან. და ბოლოს, ეს უნდა დაეხმაროს თქვენს გუნდს მოთხოვნების განსაზღვრასა და ორგანიზებაში. ამის ნაცვლად, ისინი წარმოადგენენ მაღალი დონის მიმოხილვას, თუ როგორ უკავშირდება გამოყენების შემთხვევები, მსახიობები და თქვენი სისტემა
რატომ არის Schottky დიოდი სასარგებლო მაღალი სიხშირის გასწორებისთვის?
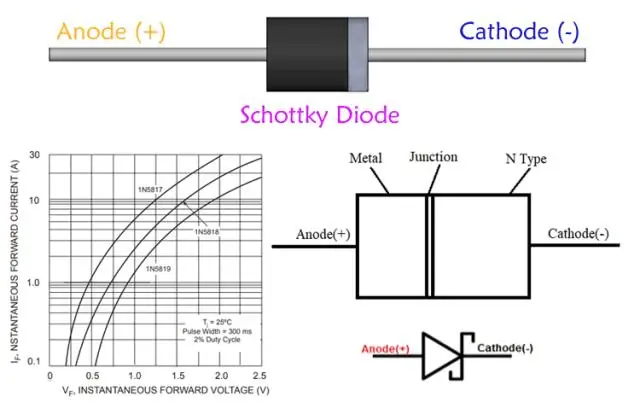
Schottky დიოდის აპლიკაციები. სიმძლავრის გამასწორებელი: Schottky დიოდები ასევე გამოიყენება Ashigh დენის გამსწორებლები. მათი მაღალი დენის სიმკვრივე და დაბალი ძაბვის ვარდნა ნიშნავს, რომ ნაკლები ენერგია იხარჯება, ვიდრე გამოყენებული იყო PN შეერთების დიოდები. შოთკიდიოდებს აქვთ მაღალი საპირისპირო გაჟონვის დენი
რატომ არის თექვსმეტობითი ნუმერაციის სასარგებლო სისტემა?
თექვსმეტობით სისტემას ჩვეულებრივ იყენებენ პროგრამისტები მეხსიერების მდებარეობების აღსაწერად, რადგან მას შეუძლია წარმოადგინოს ყოველი ბაიტი (ანუ რვა ბიტი) როგორც ორი თანმიმდევრული თექვსმეტობითი ციფრი, ნაცვლად რვა ციფრისა, რაც მოითხოვება ორობითი (ანუ ბაზის 2) რიცხვებისთვის და სამი ციფრი, რომელიც საჭირო იქნება ათობითი
რატომ არის გენერატორები სასარგებლო?
გენერატორები პითონის მნიშვნელოვანი ნაწილია მას შემდეგ, რაც ისინი შემოიღეს PEP 255. გენერატორის ფუნქციები გაძლევთ საშუალებას გამოაცხადოთ ფუნქცია, რომელიც იქცევა როგორც იტერატორი. ისინი პროგრამისტებს საშუალებას აძლევს შექმნან იტერატორი სწრაფი, მარტივი და სუფთა გზით. იტერატორი არის ობიექტი, რომელიც შეიძლება გაიმეოროს (დააბრუნოს)
რატომ არის სასარგებლო დისკის დეფრაგმენტატორი?
დეფრაგმენტაცია ჰგავს სახლის დასუფთავებას თქვენი კომპიუტერისთვის, ის აგროვებს ყველა მონაცემს, რომელიც გავრცელებულია თქვენს მყარ დისკზე და ისევ ათავსებს მათ. რატომ არის მნიშვნელოვანი დეფრაგმენტაცია? იმის გამო, რომ ყველა კომპიუტერი განიცდის ფრაგმენტაციის მუდმივ ზრდას და თუ თქვენ არ ასუფთავებთ სახლს, თქვენი კომპიუტერი განიცდის