ვიდეო: ჩართავთ თუ არა გარე მნიშვნელობებს სტანდარტულ გადახრაში?
2024 ავტორი: Lynn Donovan | [email protected]. ბოლოს შეცვლილი: 2023-12-15 23:49
Სტანდარტული გადახრა არასოდეს არის უარყოფითი. Სტანდარტული გადახრა მგრძნობიარეა გამოკვეთილები . სინგლი გამოკვეთილი შეუძლია აწიოს სტანდარტული გადახრა და თავის მხრივ, ამახინჯებს გავრცელების სურათს. დაახლოებით იგივე მნიშვნელობის მქონე მონაცემებისთვის, რაც უფრო დიდია გავრცელება, მით მეტია სტანდარტული გადახრა.
ამ მხრივ, იყენებს თუ არა სტანდარტული გადახრა outliers?
თუ მნიშვნელობა არის გარკვეული რიცხვი სტანდარტული გადახრები საშუალოდან მოშორებით, ეს მონაცემთა წერტილი იდენტიფიცირებულია როგორც გამოკვეთილი . ეს მეთოდი შეიძლება ვერ აღმოაჩინოს გამოკვეთილები იმიტომ რომ გამოკვეთილები გაზრდის სტანდარტული გადახრა .რაც უფრო ექსტრემალურია გამოკვეთილი , მით უფრო სტანდარტული გადახრა გავლენას ახდენს.
ანალოგიურად, რა ითვლება გამოკვეთად? გამოკვეთილი . მაგალითად, ზემოაღნიშნულ ფიგურაში მარცხნივ მდებარე წერტილი არის an გამოკვეთილი . მოსახერხებელი განმარტება ა გამოკვეთილი არის წერტილი, რომელიც ეცემა 1,5-ჯერ მეტ მეოთხედულ დიაპაზონს მესამე მეოთხედის ზემოთ ან პირველ მეოთხედზე ქვემოთ. გამოკვეთილები ასევე შეიძლება მოხდეს მონაცემთა ორ ნაკრებს შორის ურთიერთობის შედარებისას.
შესაბამისად, რამდენი სტანდარტული გადახრებია გამოკვეთი?
მნიშვნელობა, რომელიც ცდება 3-ის ფარგლებს გარეთ სტანდარტული გადახრები არის განაწილების ნაწილი, მაგრამ ეს არის ნაკლებად სავარაუდო ან იშვიათი მოვლენა 370 ნიმუშიდან დაახლოებით 1-ში. სამი სტანდარტული გადახრები საშუალოდან პრაქტიკაში იდენტიფიცირებისთვის ჩვეულებრივი წყვეტაა გამოკვეთილები გაუსიანური ან გაუსის მსგავსი განაწილებით.
რა არის 1.5 IQR წესი?
ინტერკვარტული წესი Outliers-ისთვის ყველაფერი რაც ჩვენ უნდა გავაკეთოთ არის შემდეგი: გავამრავლოთ ინტერკვარტილური დიაპაზონი ( IQR ) ნომრით 1.5 . დამატება 1.5 x ( IQR ) მესამე მეოთხედამდე. ამაზე მეტი ნებისმიერი რიცხვი საეჭვოა. გამოკლება 1.5 x( IQR ) პირველი მეოთხედიდან.
გირჩევთ:
ითვლის ფუნქცია ნულ მნიშვნელობებს?
მაგალითი - COUNT ფუნქცია მოიცავს მხოლოდ NOT NULL მნიშვნელობებს ყველას არ ესმის ეს, მაგრამ COUNT ფუნქცია დათვლის მხოლოდ იმ ჩანაწერებს, სადაც გამოხატულება არის NOT NULL COUNT(გამოხატვაში). როდესაც გამოთქმა არის NULL მნიშვნელობა, ის არ შედის COUNT გამოთვლებში
როგორ გაუმკლავდებით NA მნიშვნელობებს R-ში?
მონაცემთა ნაკრების სხვა სტატისტიკური აპლიკაციებიდან იმპორტის დროს, გამოტოვებული მნიშვნელობები შეიძლება იყოს კოდირებული რიცხვით, მაგალითად 99. იმისათვის, რომ R-მ იცოდეს, რომ ეს მნიშვნელობა აკლია, საჭიროა მისი ხელახალი კოდირება. კიდევ ერთი სასარგებლო ფუნქცია R-ში დაკარგული მნიშვნელობებთან გამკლავებისთვის არის na. omit() რომელიც წაშლის არასრულ დაკვირვებებს
როგორ ადარებთ რუკის მნიშვნელობებს?
ღირებულების თანასწორობის რუქების შედარების სწორი გზაა: შეამოწმეთ, რომ რუქები იგივე ზომისაა(!) მიიღეთ გასაღებების ნაკრები ერთი რუქიდან. თქვენ მიერ მოძიებული ნაკრებიდან თითოეული გასაღებისთვის, შეამოწმეთ, რომ ამ გასაღებისთვის თითოეული რუკიდან ამოღებული მნიშვნელობა იგივეა (თუ გასაღები არ არის ერთ რუკაზე, ეს არის თანასწორობის სრული წარუმატებლობა)
გარე შეერთება იგივეა, რაც სრული გარე შეერთება?
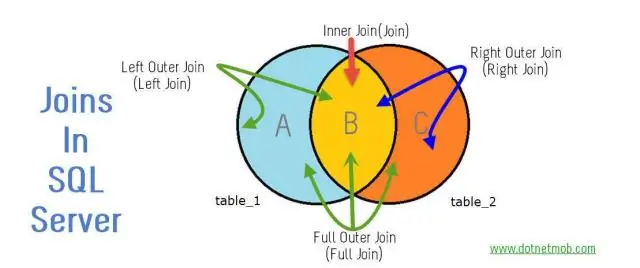
გარე შეერთებისას, ორივე ცხრილის ყველა დაკავშირებული მონაცემი სწორად არის გაერთიანებული, პლუს ყველა დარჩენილი სტრიქონი ერთი ცხრილიდან. სრულ გარე შეერთებებში, ყველა მონაცემი გაერთიანებულია სადაც ეს შესაძლებელია
რომელი ტიპის კავშირის გამოყენება შეუძლია სტანდარტულ შეზღუდულ მომხმარებელს SAP HANA მონაცემთა ბაზასთან დასაკავშირებლად?
მათ შეუძლიათ მონაცემთა ბაზასთან დაკავშირება მხოლოდ HTTP/HTTPS-ის გამოყენებით. შეზღუდული მომხმარებლებისთვის ODBC ან JDBC-ის საშუალებით დაკავშირება, კლიენტის კავშირებზე წვდომა უნდა იყოს ჩართული SQL განაცხადის ALTER USER ENABLE CLIENT CONNECT ან მომხმარებლისთვის შესაბამისი ოფციის ჩართვით SAP HANA კაბინაში